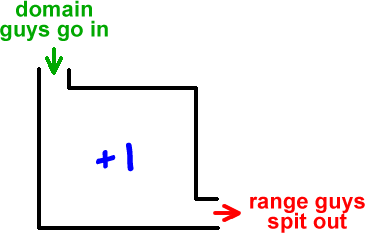
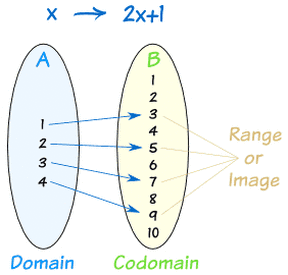
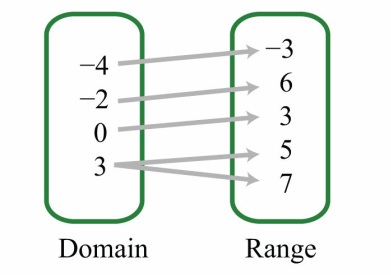
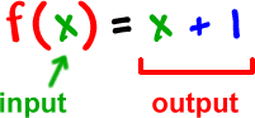For Example...
|
Each input (domain, x) has only ONE output (range, y). Each number in the domain only has one arrow coming from it, meaning it only has one output.
|
All inputs (domain, x) have one output (range, y) EXCEPT 3. You see that 3 has two arrows, pointing to 5 and 7. This means the input 3 has two outputs, making two points, (3,5) and (3,7) rather than one.
|
Try This
Brianna is growing a blueberry bush. When she bought it, it had 4 blueberries already ripe. Every day, one more blueberries ripened. How many blueberries will Brianna have after 6 days? Show domain and range and explain why it is or is not a function. Is it linear or exponential?
To find this, we can write a recursive formula. To do this, we must know our first term: 4. So, t1 = 4. The next step is to come up with a formula. Since Brianna starts with 4 blueberries, we can put that as the y intercept. The blueberries ripen at a constant rate of +1 per day, days being the variable. The function would be tn = tn-1 +1. Since we are using recursive, you would have to find every term before 6 to find how many blueberries are ripe in 6 days. So, we will make a chart.
To find this, we can write a recursive formula. To do this, we must know our first term: 4. So, t1 = 4. The next step is to come up with a formula. Since Brianna starts with 4 blueberries, we can put that as the y intercept. The blueberries ripen at a constant rate of +1 per day, days being the variable. The function would be tn = tn-1 +1. Since we are using recursive, you would have to find every term before 6 to find how many blueberries are ripe in 6 days. So, we will make a chart.
|
Days (x)
1 2 3 4 5 6 |
Blueberries (y)
1 2 3 4 5 6 |
You already know the constant rate of change is +1 per day, so to make this chart, you'd do that: add one more than she had the day before.
This problem is an example of a function. Each input only has one output. It is linear because there is a constant rate of change using addition. Our formula for this would be f(x)=x-1+1, simplified to f(x)=x. All you have to do is plug in the day you are looking for into the x. So, after 6 days, Brianna will have 6 ripened blueberries. |
But, What If...?
What if you could solve the problem without having to find all previous terms? You would write an exponential function. With Brianna's blueberries, you can't do this because you have to add one to the previous term, but you could write an exponential function with a problem like this:
John is growing bacteria for a science project. He starts with 10 bacteria on the first day. Each day after that, the bacteria number doubles. How many bacteria will he have on the sixth day? Show domain and range and explain why or why not it is a function. Is it linear or exponential?
Now, we can write an exponential function. We still use the same outline as a linear function- f(x) - but instead of using mainly addition, exponential deals with exponents. We will use x as days. We will still have to know the previous day, and we will soon make a recursive formula. First, let's make a chart.
John is growing bacteria for a science project. He starts with 10 bacteria on the first day. Each day after that, the bacteria number doubles. How many bacteria will he have on the sixth day? Show domain and range and explain why or why not it is a function. Is it linear or exponential?
Now, we can write an exponential function. We still use the same outline as a linear function- f(x) - but instead of using mainly addition, exponential deals with exponents. We will use x as days. We will still have to know the previous day, and we will soon make a recursive formula. First, let's make a chart.
|
Days (x)
1 2 3 4 5 6 |
Bacteria (y)
10 20 40 80 160 320 |
To make this chart, we will have to find the function. Since John has 10 bacteria on the first day, and it doubles each day, our rule would have to be 2 to the x power. This means our function would also be f(x)=2^x, because you still have to know the previous day to find the next.
Now we will write our recursive formula. We know that tn=1. Since we know the function, we can easily write the formula. The formula is tn=tn-1(2). |